A number of important ideas have informed my 50+ years of teaching and research in computer science, at universities, research laboratories, conferences, and workshops around the world. This page consist of essays that describe and trace the evolution of several of these ideas:

• The emergence of online learning as an effective and efficient means to vastly expand access to education.
• The development of computer science as an academic discipline that is relevant to every educated person in the 21st century.
• Discovering and learning fundamental practical algorithms and effectively applying that knowledge through algorithm science.
• Visualization as a tool to understand algorithms and data structures.
• A calculus for learning properties of discrete structures known as analytic combinatorics, developed with my late friend Philippe Flajolet.

Remarkably, many of these topics have remained relevant for decades, and are likely to remain relevant in the future.

Online Learning

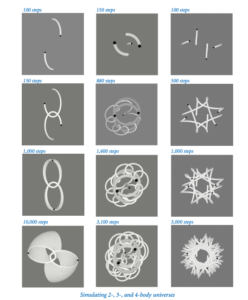
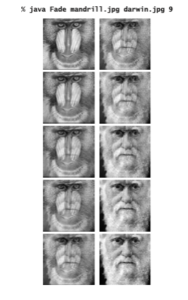
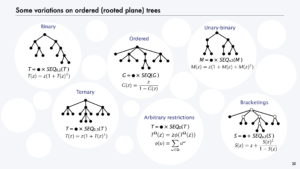
One of the main reasons one enters academia is to play a role in disseminating knowledge. My career as an academic coincided with revolutionary developments in technology culminating in the development (with my colleague Kevin Wayne) of a new model for disseminating knowledge. We have created an extensive amount of content (see the COURSES page here for access to it) and have been using it to reach millions of people worldwide.

A 21ST-CENTURY MODEL
FOR DISSEMINATING KNOWLEDGE

Textbooks. A central focus of my career since 1975 has been creating textbooks. People in my generation had the unique challenge of teaching without the benefit of the time-tested textbooks that our peers in other fields throughout the university were depending on. This turned into a unique opportunity—many of us were able to define the field by writing textbooks.
     My books have sold over one million copies. On the basis of the experience of creating them, I know that a good textbook has the following features:

• Serves as guiding force and “ground truth” for students learning a core subject.
• Distills a lifetime of faculty experience for future generations.
• Provides a reference point for courses later in the curriculum.

These features still have substantial value, and textbooks are here to stay. Some people might prefer electronic versions, but a substantial number prefer physical textbooks (or both). One possible reason: Printed books enjoy the benefit of 500 years of development since Gutenberg while online content has only been around for several decades.

Booksites. Still, online content can vastly leverage printed material in at least the following ways:

• Provide readily accessible presence on the web.
• Allow for regular updates and extensions.
• Provide content types not feasible in print, such as production code, test data, and animations.

These features have substantial value–online content is here to stay.
     Why not just put the book online, as an e-book? Because it was not designed to be read online! For decades, I have been learning how to present the content on the printed page in the best possible light and how to create detailed figures that supplement the text (see the Visualization tab here). Yes, appealing presentation of content is also important for the booksite, but its main purpose is to facilitate searching, following links and scrolling on a variety of devices and to provide access to content types not possible on the printed page. Development of best practices for online content is still a work in progress (and a few centuries behind developments for the printed page).
     Not long after he arrived at Princeton in 1998, Kevin Wayne conceived of the idea of organizing and developing the content for our introductory computer science course online, for immediate use by our students, but also in anticipation of using it for a book someday. The booksites that Kevin and I have developed over the next two decades now consist of tens of thousands of files and have attracted tens of millions of page views. They are unique and valuable resources. A good way to understand what they can contribute is to spend some time browsing through them.

Computer Science: An interdisciplinary approach
Algorithms (4th edition)
Analysis of Algorithms
Analytic Combinatorics

Lecture Videos. Even more ubiquitous than a textbook is the idea of a lecture. Faculty and students regularly gather together, often in a large lecture hall, for the lecturer to present material to the students so that they may learn it. This model has been an essential part of education for a very long time because it

• Allows instructors to communicate directly with students.
• Stimulates the development of a “community of scholars”.
• Encourages great teachers to inspire large groups of students.

These features have substantial value, and lectures are here to stay.
     But it is not necessary for everyone to gather at the same place and time. It has long been recognized that large live lectures have substantial drawbacks because they

• Require significant time and effort for preparation, which is largely duplicated by instructors around the world.
• Place students in a passive role, just listening to the lecture (and maybe taking notes).
• Move at one fixed pace, which cannot be the right one for all students. Most students in a large live lecture are absent, lost, or bored.

Despite these obvious and well-researched drawbacks, large live lectures are the overwhelmingly predominant method of instruction in US universities and many other educational institutions.
     By contrast, making well-produced videos of lectures available to students encourages them to

• Actively choose the time and place they learn. No one is absent.
• Actively choose their own pace. Students can speed up the video if bored or slow it down if lost.
• Review the lecture at any time. Students can review material until they understand it, and refer back to it for exams.

Once one has experienced the ability to consume lectures when and where one wants, going back to having to be at a particular time and place to hear a lecture seems antiquated. It’s like the difference between having to watch Seinfeld at 9PM on Thursday nights and binge-watching episodes on a whim.
     It is true that lectures have to be well produced. I spent 50-100 hours of preparation for each lecture and needed skill in using Unix, emacs, OS X, Dropbox, Illustrator, Keynote, TeX, HTML, MathJax, Mathematica, PostScript, and a dozen other tools I can’t even name. But it was less time-consuming than writing a book.
     The most important development for the future, which is just starting to take hold, is that faculty will adopt online lectures prepared elsewhere instead of preparing and delivering their own, freeing up time for them to decide what material they want their students to learn, to appropriately assess their progress, and to help them succeed.

Online services. In recent years, there has been explosion of research and development in educational technology. I have only been peripherally involved, but it is appropriate to mention here some of the tools that we have been using:

• Websites built with HTML that provide all course information for students.
• Tigerfile for managing programming assignment submissions.
• codePost for grading programming assignments.
• Zoom for class and precept meetings and office hours.
• Gradescope for online exams.
• CUbits to curate, serve, and monetize lectures.
• Quizzera for online quizzes.
• Coursera for free online MOOCs.
• Safari for access to content in a corporate setting.
• Ed for student Q&A and peer discussion.
• E-mail for authoritative communication from faculty to students.

Taken together, such tools comprise a fourth component of our model as they have allowed us to effectively scale our offerings to reach large numbers of students. The suite of available tools is constantly evolving and remains an exciting area of research and development. Their true potential is yet to be realized.

HISTORICAL PERSPECTIVE

I could write a book on this topic, but I’ve written enough books, and it’s not really my area of research expertise. Instead, my intent is to provide context that can help explain the evolution of my thinking on these matters. Much of my thinking stems from a series of invited talks that I gave around the world in the years before the pandemic.

Origins. For more than a century, faculty at colleges and universities would disseminate knowledge by writing papers and books, delivering large live lectures, and leading small groups of students in discussion or problem-solving sessions. In the 1970s, things began to change.

Desktop publishing. My thesis was written out by hand and typed by a secretary, as were my early papers. The process could take over a year. In the span of a decade (the 1970s, roughly) the infrastructure that we enjoy today emerged, where dissemination can be achieved in an instant. I was fortunate to have the opportunity to play a role in this revolution, first at Xerox PARC and later at Adobe. It is hard to overstate the impact of experiencing these changes as an academic. We could write detailed class notes and assignments instead of writing problems on the board in class, and the time between finishing a paper or a book and publishing it shrank from a year or more to a month or less. More important for me was the fact that the entire creative process was in my hands, not left to a secretary or a printer. This aspect of desktop publishing was controversial to some. Didn’t faculty have more important things to do than to worry about fonts and the like? Maybe, but a surprising number of talented computer scientists, from Knuth and Kernighan to Simonyi and Warnock, dedicated themselves to advancing this art, and we are all in their debt. Personally, I spent much of the 1980s and 1990s using state-of-the-art digital publishing tools to create my Algorithms books.

A dream realized. By the turn of the century, it was clear that the internet and the personal computer were going to play a dominant role in the dissemination of knowledge. But the idea had been envisioned half a century earlier, by Vannevar Bush. In 1997, I delivered a speech to Princeton’s first-year class telling that story. This speech is still remarkably relevant today. When Google revolutionized the internet a year later, the last piece of Bush’s vision was realized. We could imagine having access to the world’s knowledge on a personal device, we could disseminate knowledge just by posting it, and anyone could have access to it.

But how, exactly? In the early years, everyone was burned by the experience of advancing technology rendering content obsolete, even lost. A new version of a text editor, or a new editor, or a new company might mean that my online contribution to knowledge would disappear. That did not happen with paper. I can still find my mother’s PhD thesis, written nearly a century ago, at the Brown library. Whatever editor or typesetting system or markup language you are using, are you sure what you are writing now will be readily available in a century? I’m not, and I consider this problem to still be open. In late 1997, I wrote a short letter to the New Yorker making this very point. Not much has changed since, really.

Booksites. As the internet came into daily use in the 1990s, first thing that faculty did was to post assignments, deadlines, exam dates and the like on course websites, a much more convenient way to handle such information than writing it on the blackboard or preparing paper handouts. Naturally, people started putting more and more content on these sites, too. But much of this content seemed specific to the course and ephemeral, when some of it was destined for a textbook.
     When Kevin Wayne began working with me in 1998, he started putting significant amounts of content on a webpage, separate from any course offering. For nearly a decade, we used this page as a development laboratory for our new textbook. Everything went on the web, but we could cherrypick the information there while creating the coherent story needed for a textbook. Once the book was published, the page became a valuable resource for readers, providing all kinds of content that unsuitable for a book. Thus was born the concept of a booksite. It was so successful that we created another one for Algorithms, which significantly increased the appeal of that book, even though it was already a bestseller. Then I did the same for Analysis of Algorithms and Analytic Combinatorics, making them much more accessible to many more people than the books alone could be.
     Our booksites now have tens of thousands of pages that draw millions of unique visitors each year and tens of millions of pageviews.

MOOCs. Should we include videos of some sort in our booksites? It is a natural idea, but it just never seemed worth the effort. Things changed in 2012 when Daphne Kollar and Andrew Ng formed Coursera and encouraged educational institutions to vastly expand their reach by putting lecture videos online. Having just revamped our lecture slides for the fifth or sixth time, Kevin and I realized immediately that they would be perfectly suited to doing this, and we produced Algorithms for the Coursera platform. It was immediately successful and has already reached over 1 million people.
     Over the next several years, I recorded over a hundred hours of videos that are the basis for six Coursera courses. For me, the appeal of these courses is that they make the content accessible to a huge number of people whoo otherwise would not have access to them. I’ve always been uneasy about the model of issuing certificates or otherwise trying to compete with existing educational institutions. My preference is to develop materials that can enable any of the millions of teachers around the world do their job more effectively and efficiently. That is what the “21st century model” is all about. Our experience is that many faculty are reluctant to have their students take a MOOC, but we are often able to convince people that watching videos in conjunction with the booksite and textbook can free time for them to work on curating the material, developing assessments, and helping their students succeed.

Moving my Princeton courses online. After recording the last lecture in our introductory course Computer Science in the early summer of 2015, I was exhausted and thought to myself that it would be very difficult for me to deliver that lecture again in the classroom. I had spent many, many hours preparing the slides for that lecture (and all the others). One of the most important aspects of the lectures was that the lecture slides were very detailed, but the information on a lecture slide would appear gradually, controlled by a remote in my hand. Creating and checking these “builds” was very time-consuming but also excellent preparation for the lecture. I didn’t need any rehearsal, as I knew what was going to appear on the screen each time I advanced the remote, and just talked about it. One of the last slides in the last lecture was a simulation of a CPU circuit, with over a hundred builds. To deliver that lecture again in a year, I would need to revisit all the decisions I made in sequencing those builds—I knew that would be a difficult and time-consuming job. And why do it? I couldn’t do as good a job as just captured in the video. And if I couldn’t do it, no one else could either.
     I knew then that the days of me or someone else reading my slides to their students in a large lecture hall were over. In September 2015, I delivered a “last live lecture” where I explained the change to the students, and haven’t looked back.

The pandemic. The full story remains to be written, but having moved my lectures online, the spring of 2019 went relatively smoothly in my courses. I promised the students that we would provide them with an experience comparable to that experienced by the thousands of students who have taken it in the past. I think that having the lectures online provided our course staff with the stability and breathing room needed to develop new ways of interacting with students and we were able to approach that ideal, despite the circumstances. My teaching ratings were among the highest I have ever earned. Moreover, plenty of students and faculty at other institutions were able to take advantage of our materials to help with their transition of online teaching.

THE FUTURE

I am often asked how the pandemic has affected my teaching. The answer is that the most important effect has been that no one hassles me about not having in-person meetings with students! My opinion is that the new ways of teaching that embrace technology are so much more effective and efficient than the old ones that do not.
     Sure, there are plenty of situations where in-person instruction is valuable. Most teachers are drawn to the profession by the pleasure of the experience of kindling the light of understanding in a student or a group of students. But insisting that all instruction be done this way and only this way is counterproductive.
     Rather than mapping out strategies to get back to old ineffective and inefficient teaching methods, we should be brainstorming ways in which we reach out to more students than ever before and taking them farther than ever before. To conclude, I’ll offer some comments on the way I do things now, in an attempt to illustrate what is possible.

Lectures. Personally, I cannot conceive of building a course based on large live lectures again. Many people have created quality video content during the pandemic and are seeing the benefits of using it. Yes, good online lectures are difficult to produce, but the investment produces a much better experience for students and is certainly worthwhile when amortized over future and expanded usage.

E-mail. This old-school technology is effective for synchronizing a course. I send an e-mail to all officially registered students each week describing their responsibilities for the week. In my experience, students take such e-mails seriously.

Personal interaction. When I was teaching in a lecture hall with 400+ students, I certainly had little personal interaction with students. Now, when I walk across campus or attend a large conference, I am often approached by a student who seems to know me. Watching lectures regularly in a private setting gives each student a sense of a personal relationship with me.

Grading. Anyone not using online tools for grading needs to rethink what they are doing. In our first-year classes, we grade hundreds of student programs in a matter of hours each week, with high standards for personal feedback and fairness. In my advanced class, I grade dozens of advanced mathematical derivations in well under an hour—speaking of personal interaction, I get to know those students relatively well. And in both classes, I can do assessments that are auto-graded. Zero time spent grading is tough to beat. And these experiences only scratch the surface, with sea-assessments and crowdsourcing already proven to be effective.

Discussion forums. Online discussion forums have replaced office hours, having proven extremely effective and efficient in helping us answer student questions. It took some experience for us to guide students in using this resource effectively, but it is now indispensible.

AND THIS is all from the perspective of decades of clinging to old ways and having to be convinced to adopt new approaches. As ever, the next generation, unburdened, will take us places we cannot even imagine today.

Professors Behind the MOOC Hype (Chronicle of Higher Education)
A 21st Century Model for Disseminating Knowledge (RS invited lecture)
A 21st Century Model for Disseminating Knowledge (video of MIT lecture)

Computer Science for All

To most people, this exhortation means “everyone should learn how to code.” I completely agree that everyone should know how to code, but I also think that most if not all college students should know fundamental concepts in computer science, which are among the most important and impactful intellectual achievements of the last century.

What is Computer Science?

One can spend a day or a week or a month studying this question. People have been debating it for many decades. I prefer to think about the definition along the following lines:

computer science

The quest for knowledge about phenomena surrounding computation, and the application of that knowledge for the betterment of humankind.

OK, “for the betterment of humankind” is unnecessary, but I’m leaving it in. When people use computation no good purpose or for evil, they can call it something else.
     Much of my career has involved grappling with the question a different way. As founding chair of the department of computer science at Princeton, I was soon faced with the need to develop a new introductory course. I strongly feel that computer science belongs in every college curriculum, like mathematics, economics, physics, biology, and other core disciplines. So I asked myself “What should every college student know about computer science?” After 25 years of work, our book (with Kevin Wayne) Computer Science: An Interdisciplinary Approach, answers this question by demonstrating that computer science is about:

• Learning to write programs in a modern programming language.
• Realizing that know one programming language makes learning another one relatively easy.
• Understanding concepts like type checking, modularity, recursion, and data abstraction, which make modern languages effective.
• Studying classic data structures and algorithms and their application in practical situations.
• Knowing how to estimate how much time and memory programs use.
• Appreciating fundamental concepts in the theory of computation: universality, computability, and intractability.
• Gaining insight into how modern computer processors are built, including complete design of a simple processor.
• Gaining insight into the strong relationships between the programs we write, the theory of computation, the computers we use, and the natural world.
• Learning the contributions of Turing, von Neumann, Boole, Shannon, and other giants.

In my view, a person who has studied these has the foundation needed to use computers effectively. Conversely, a person lacking this basic knowledge will struggle to compete in today’s world.
     Many years ago, people debated whether CS is a science at all, and whether it deserves any place at all in the college curriculum. An acquaintance once told me that one of his colleagues made this argument on the floor of his faculty senate:


“A computer is a useful man-made artifact, like a refrigerator. We don’t have a department of refrigerators, so why should we have a department of computer science?”

Sure, CS is useful and interesting, the argument would go, but what does it tell us about the universe? Fortunately, amazing progress across the board has left such arguments by the wayside. Now, there’s little question that computation is not just useful but also underlies many natural processes, and that understanding computer science is the key to progress in many other fields of science.

One Course
Even in the 1960s, scientists realized that computers were going to be indispensable in their work, so courses would spring up in every department to teach students what they needed to know for later courses. But these courses often suffered from a “department of refrigerators” attitude and essentially were replacing labs that used slide rules and calculators with labs that used computers. And they were doing it far too slowly. For example, I was horrified to realize that my son, a potential physics major at Princeton, spent an afternoon in the lab computing the mean and standard deviation of a bunch of numbers on a calculator, in 1994 (!).
     The attitude that the computer is nothing more than a tool persists to this day in many circles. As a result, many universities, offer several courses in computing, one or more per department, each serving potential majors in that department. This approach is flawed because:

• The courses teach programming in a specific language, not computer science.
• They are not taught by professors of computer science, while introductory courses in other disciplines are taught by professors in that discipline.
• They do not prepare students for later courses in computer science. This is the most important flaw.

I was determined to change this at Princeton and to try to develop an existence proof for others. Little did I know that it would take over 25 years to do so.
     Computer scientists can be often part of the problem, too. All around the world, many people have been orienting their introductory course towards future cubicle dwellers and ignoring the needs of others. Indeed, at many prominent institutions, enrollment in computer science courses is strictly limited, leaving most students wholly unprepared with respect to computing. I consider this to be responsible and bordering on the immoral.
     Up until the 1980s, Stanford did not offer an undergraduate CS degree and would counsel students to study something else as an undergraduate and take CS as a graduate student. While not a “department of refrigerators” attitude, I can attest to the fact that it certainly made building new departments at Brown and Princeton more challenging.
     From the beginning, I was determined to build a single CS course at Princeton for first-year students that was open and accessible to everyone, like introductory courses in other disciplines. We would teach fundamental concepts in the discipline and develop skill in exploiting the power of the computer. Our examples and assignments would all address interesting practical problems, ideally in some other discipline, while at the same time teaching some fundamental CS concept. To get this going, I asked students majoring in other subjects to bring back to us problems in their disciplines where computing should play a central role. They brought back many exciting examples, thus illustrating the broad reach of computing, even to the cubicle dwellers.
     One immediate roadblock was the lack of a suitable textbook that could command the respect accorded classic texts in other fields. From the beginning, development of the textbook has gone hand-in-hand with development of the course. Indeed, the effort went far beyond just a textbook, once Kevin Wayne joined the effort. During the 2000s, we developed extensive online content for the course, and during the 2010s, we put the lectures online, which are now available for use around the world. Finally, in 2016, our textbook Computer Science: An Interdisciplinary Approach was published.

Progress Report

I was optimistic from the start, but success has been at a scale I could not imagine. In the 20th century, students would say that taking a course in computing is bad for your social life. Now, at Princeton it is the case that not taking a course in computing is bad for your social life. For many years, it has been the highest-enrolled course at Princeton.
     Beyond the success of the course itself, the downstream impact has been way beyond expectations:

• Our second course (Algorithms) is also consistently among the top five highest-enrolled courses at Princeton.
• CS is the highest-enrolled major at Princeton.
• Thanks to our 21st century model for disseminating knowledge, other institutions around the world are able to adopt this approach.

Yes, enrollments are up everywhere, and there are some universities that have matched this level of success, but nationwide totals show that a large majority of institutions are not coming close to adequately serving their students with appropriate CS instruction.
     To reiterate, my position is that “CS for All” has to begin with an introductory college course suitable for all students, based on a textbook that covers the fundamentals, to prepare student for success in a lifetime of engaging with computation, whatever their chosen pursuit. I set out to prove this concept in 1992 and am now declaring victory.

The Discipline that is Transforming Higher Ed (Chronicle of Higher Education)
Computer Science for All, Really (Princeton CS Department)

Algorithm Science

[latexpage]

This terminology might seem a bit odd to many people at first blush, but when I tried it out on a some colleagues, they agreed that it perfectly describes the main thrust of the field of research introduced by Don Knuth and his books The Art of Computer Programming (to which I have devoted my career). His name for the field is “analysis of algorithms.” With respect, I now feel that “algorithm science” is much more descriptive and appealing.
     I wish I had thought of this decades ago. My book Introduction to the Analysis of Algorithms with Flajolet might be named Mathematical Methods for Algorithm Science, as would our international AofA and ANALCO meetings. And the chapters in Algorithms and Computer Science that cover the basics might be titled Algorithm Science.
     I am writing about this here because I think that this field of research deserves more attention as it has been foundational in the development of our vast computational infrastructure.

The problem. Everyone using a computer has often wondered how much time a given program will need to finish its job. In many cases, such as adding a column of numbers in a spreadsheet, the computer is so fast that the time taken is negligible, but in many other cases, such as a guidance system in an airplane, it is critically important to be able to guarantee that the computation will finish on time. It is about as easy to write a slow program as a fast one. Is there a systematic way to be able to tell the difference?

Algorithms. Large software systems can be very complex, but it is often the case that studying performance reduces to the study of particular core computational problems that have been the subject of decades of research, the kind of material covered in my Algorithms books. The idea of an algorithm separates a computation from a particular device. An algorithm is a step by step description of a computation that a developer can use to implement a program on any given computer. The time needed by the program certainly depends on the system and the computer, but properties of the algorithm are also relevant. By studying such properties, we can gain insight and understanding about the algorithm, and, by extension, any implementation. It is typically easy to identify important properties. How many comparisons does a sorting algorithm use? How many edges are examined by a graph-processing algorithm?

Algorithm engineering. The process of implementing an algorithm on an actual computer is quite simply called programming. In mission-critical applications, the process is a bit more sophisticated and often called algorithm engineering. Loosely speaking, algorithm engineering is the process of choosing and implementing an algorithm to address a particular application on a particular machine, with careful attention to performance. Most serious program development involves algorithm engineering, and most programmers love to do it. Typically, the process ends with an “optimization” phase, where a programmer finds a way to improve performance by matching match some property of the algorithm to a capability of the machine.
     Unquestionably, people who build computer systems pay attention to performance. No one would buy a cellphone that takes a minute to wake up if a similar one takes just a second. So system builders test performance extensively by running experiments to see how much time is needed to complete tasks that their customers care about. This approach is successful and widely deployed. Nowadays, people rely on standardized benchmarks run by trusted third parties to decide whether a new computer is sufficiently faster than an old one to be worth the expense.
     One drawback is that people may be drawn to “designing to the benchmarks”. One extreme example of this is “Timsort”, which was hailed for a time as being novel and faster than any other sorting algorithm because of its performance on benchmarks. Closer examination showed that it adopted a well-known approach that performed exceedingly well on a few of the benchmarks, and that it actually was not even correct. It uncovered a shortcoming in the benchmarks, not a new algorithm.
     A better approach is to take advantage of understanding both the algorithm and the machine instead of relying completely on benchmarks. While useful, benchmarks, on their own, generally do not provide much insight or understanding about what is actually happening.

Theory of algorithms. A widely-accepted theory classifies algorithms by developing bounds on their worst-case performance. This approach provides an appealing framework based on simple mathematical tools and has supported a Golden Age of Algorithm Design. The drawback is that it does not provide enough information to be able to predict performance in practice or to compare algorithms. The constant factors matter, and, worse, the input is typically not the worst case. The most important reason for practitioners to be skeptical of results in this literature is that many, many authors ignore or are unaware of these facts.
     Typically, algorithms developed in this community have but one purpose: to enable the proof of a theorem. As such, they can become exceedingly complicated and arcane—no one should consider implementing them. As my late friend Philippe Flajolet once put it:

A large fraction of the theoretical computer science research community reverted to worst-case analysis based on simple tools from computational complexity. In all too many cases, this has resulted in an excess of its own, with works culminating in teratological constructions both devoid of mathematical simplicity and elegance and bearing little relevance to the practice of computing.

To save you the trouble of looking up the definition of “teratological”, here it is:

teratological

1. abnormal in growth or structure.
2. of or relating to teratology.

teratology

1. The scientific study of congenital abnormalities and abnormal formations.
2. Mythology relating to fantastic creatures and monsters.

Philippe told me that he was proud of this word choice as it leaves ambiguous whether one considers this type of algorithm to be abnormal or just a fantastic creature. Certainly his point is that such algorithms have little to do with the real world.

ALGORITHM SCIENCE

In algorithm science, we take a middle road between pure benchmarking and pure theory. A problem with the theory of algorithms is that it pays too little attention to the real world; a problem with benchmarks studies is that they pay too much attention to the real world. The middle road, the goal of research in algorithm science, is to learn properties of algorithms that can support algorithm engineering and experimental studies in practical situations, independent of any particular machine. More formally, I propose this definition:

algorithm science

The application of the scientific method for the design and analysis of algorithms—developing mathematical models for characteristics of algorithms and their inputs, formulating hypotheses relevant to the study of performance on specific classes of computers and systems, running experiments to validate the hypotheses, and iterating as appropriate with the goal of improving performance.

The scientific method. Since the enlightenment, our understanding of the world in which we live has expanded dramatically because of universally accepted principles about how to learn things and gain confidence that they are true. Applied to the study of computer programs, these principles lead to the following intuitive approach.

• Create a mathematical model.
• Develop a hypothesis about real-world performance.
• Run experiments to validate the hypothesis.
• Iterate on the basis of facts learned.

Each of these steps presents significant challenges in any scientific endeavor. The irony is that they can be easier in algorithm science than in many other sciences.

Mathematical models. The starting point is to identify properties of the algorithm to be studied. Knuth does this by assigning variable names to the frequency of execution of each instruction in the program. Then the mathematical model is simply a linear combination of these variables: the sum over all instructions of the product of the frequency of execution and the cost.
     Understanding costs require understanding of a particular computer system. This is the worthy and important goal of algorithm engineering, where researchers seek to leverage that understanding to develop improved implementations. Importantly, it is not always necessary to know much about the variables to improve performance, because reducing the total cost by reducing costs for the most frequently executed instructions is often effective. But this approach has limitations (for example, when there are tradeoffs between different groups of instructions with similar costs) that can be addressed with the help of algorithm science.
     The values of the variables are dependent on the inputs to the algorithm. The model must take properties of the inputs into account, as must any experiments. By just developing bounds on the worst case, the theory of algorithms avoids this problem. In algorithm science and engineering, learning properties of the inputs to be expected in practice is an essential first step. Often, we are able to assume that the inputs are random in some sense, or to add randomization to the algorithm, so that our analysis becomes probabilistic. Of course, any such assumptions need to be checked by experiments on “real” inputs of the type that might be expected in practice (benchmarks).
     Frequency-of-execution variables are the focus of algorithm science. We build mathematical models describing their values given certain assumptions about the inputs and then run experiments to test those assumptions and refine the models. Knuth has taught us that such models can lead to fascinating intellectual challenges.

Experiments. We can simply implement the algorithm, instrument it to determine the values of the variables, and collect results. Many systems provide profiling capabilities to automate this task. Experiments are relatively cheap. Unlike some other scientists, we don’t have to kill animals or send equipment to space or anything of the sort. We can actually run millions or billions of experiments with ease. For this reason, it is typical in algorithm science to run the experiments first and use the results to help develop an appropriate mathematical model.
     Importantly, one reason that many, many algorithms developed in the theoretical computer science community are not susceptible to algorithm science is that no one has implemented them (or would want to, or even could). In algorithm science we take the point of view that we want to study algorithms that have the potential to be useful in practice. To paraphrase Knuth: “If I can’t run it on my computer, I’m not interested in studying it.” His books are testimony to the fact that there are many, many algorithms in this category.
     In the scientific method, the hypothesis is not useful unless it is falsifiable. That is, it must be possible to conceive of an experimental observation that disproves the idea in question. This is a key distinction between algorithm science and the theory of algorithms. Falsifiable hypotheses are hard to come by in the theory of algorithms; they are central to algorithm science.

Approximations. At the beginning of my career, I was very excited to see that we could develop exact models that can predict results with full precision. It was particularly exciting to capture oscillatory behavior.
     In many, many practical situations, analyzing the leading term is enough, and provides much more insight than running experiments alone. A better focus on useful approximations early on would have been helpful in expanding the use of algorithm science. Unfortunately, much of the research community in theoretical computer science settled on approximations that are not particularly useful in studying performance in practice.

O-notation considered harmful. For many years, I included a slide with this title in my lectures and talks describing this encounter with a superstar researcher at a conference on the theory of algorithms:

SS: Algorithm A is bad. Google and Facebook should be interested in my new Algorithm B.
RS: What’s the matter with Algorithm A?
SS: It is not optimal. It has an extra O(log log N) factor.
RS: But Algorithm B is so complicated as to be unimplementable, lg lg N is less than 6 in this universe, and that is just an upper bound. Algorithm A is certainly going to run 100 times or more faster in any conceivable real-world situation. Why should Google and Facebook care about Algorithm B?
SS: Well, I like it. I don’t care about Google and Facebook.

And I can testify that the audience seemed to be on his side, not mine. Just to be clear: I thought the paper was an insightful mathematical contribution. But I felt strongly enough that it is very misleading to claim relevance to practical computing that I was willing to confront a superstar.
     In this case, the hypothesis that Algorithm A is faster than Algorithm B is falsifiable. One could conceive of implementing them and learning that B is 100 times faster, but would that be a worthwhile endeavor when the outcome is so patently obvious?
     Worse, use of O-notation very often leads to hypotheses that are not correct and also not falsifiable in practice.
An alternative to O-notation. Suppose that A_N is a variable that represents the running time of a program with N inputs and that we can prove that A_N / N² approaches a constant as N grows. Here are two ways to express that fact mathematically:

theory of algorithms     A_N = O(N²)
algorithm science         A_N = cN² for some constant C.

We use the more precise notation of algorithm science because it enables us to develop machine-independent falsifiable hypotheses.
     The simplest such hypothesis is the doubling hypothesis. In this case, the hypothesis would be “If you double the size of the input, the increase in the running time will approach a factor of 4.” This hypothesis is machine-independent and falsifiable.
     And it goes both ways. If your program takes four times as long to finish when you double the size of the input, a reasonable hypothesis is that its running time is quadratic.
     I wish I had thought of this years earlier than I did, but at least it has made it into my Computer Science and Algorithms books as a very simple way for any programmer to gain some understanding of running time.

Advice for practitioners. My purpose is not to be critical of anyone but to help practitioners navigate a huge literature filled with misleading claims, actual and implied.
     If you’re looking for a solution to a practical problem and run across a paper that claims an algorithm to be practical based on a O- analysis but exhibits no evidence of anyone ever having implemented it, I’d ignore it. Do you really want to be the very first person to ever implement an unproven algorithm? Believe me, I have done it many times and cannot recommend the experience.
     It is unwise to ignore performance during development. Typically, software systems need to be scalable, and you should know if you’re heading down the path towards unacceptably bad performance. Using the doubling hypothesis is not very difficult and can help avoid surprises later on.

THE prototypical example. Anyone dubious or confused about these ideas would do well to read C.A.R. Hoare’s 1960 paper Quicksort, where he introduced the algorithm that remains today the sorting method of choice and provided an analysis that exemplifies algorithm science.
     After describing the algorithm, he introduced the idea of randomization and then provided a mathematical analysis showing that the expected number of compares for random keys is ~ 2N ln N and the expected number of exchanges is one-sixth the number of compares, so that the running time is ~ cN ln N for some machine-dependent constant. With doubling, we can pose this machine-independent hypothesis:

If you double the number of the inputs, the running time of Quicksort will increase by a factor of about 2 + (2\ln2)/ln N.

While he didn’t explicitly state this hypothesis, Hoare’s paper implicitly describes a doubling test, as he gives running times T_n for files with N random keys that double from 500 to 2000. It is amusing to calculate that these values validate the hypothesis.

     If you want to validate the machine-independence of the hypothesis, you can download Quicksort from our booksite and test it on your own computer for thousands or millions of times as many inputs. Hoare’s paper is the prototypical example of algorithm science because it is just as useful in predicting performance on todays computers as it was on the particular computer he was using in 1960 (and all those developed in between, not to mention those developed in the future).
     Note that the assumption that the keys are random may not hold in some situations. Rest assured that variants of the algorithm have been studied and tested that handle such situations. The most prominent such case is when large numbers of equal keys have are present—see the RESEARCH page here.

Bottom line. Algorithm science has played a critical role in the development of our computational infrastructure, and continues to do so. From Google to genomics, the progress we have seen over the past several decades would not have been possible without algorithm science. Admittedly, no one has been calling their work algorithm science, but if it walks like a duck… Certainly, the most successful endeavors have been based on extensive mathematical modeling and experimentation, often exploiting knowledge about foundational classical algorithms.
     I would say that algorithm science is in its infancy, but I was there when it actually was in its infancy—-when professional programmers coded in assembly language while binary search and linked structures were the province of pointy-headed intellectuals. Let’s say that algorithm science is in its teenage years. There are many, many, great algorithms waiting to be discovered and studied.

Further reading. The possibility of algorithm science was firmly established by Knuth. One cannot read The Art of Computer Programming without coming away with a full appreciation for the idea. Yes, the books do lack implementations in a mainstream programming language, but there is no question that there is sufficient detail to develop and study implementations with a proper scientific attitude.
     You can find a thorough introduction to algorithm science in the context of a particular example in Chapter 1 of my book with Flajolet An Introduction to the Analysis of Algorithms. Our intent in writing this book was to provide for students the mathematical background necessary to appreciate Knuth’s work (and to be able to properly study algorithm performance).
     To see the importance of algorithm science laid bare in the context of an industrial-strength system, read about LEDA, by Mehlhorn and his collaborators.
     The third and fourth editions of my Algorithms books are filled with examples. Pick your programming languge: C, C++,or Java. As I realized that more and more people were using my code when building systems, I thought it irresponsible to be recommending particular algorithms and implementations without using the scientific method to build confidence in the recommendations I was making. More details on this story are on the RESEARCH page here.
     Other outstanding examples of algorithm science are found in Bentley’s Programming Pearls books and Sequential and Parallel Algorithms and Data Structures: The Basic Toolbox by Sanders, Mehlhorn, Deitzfelbinger, and Dementiev.

Visualization

Analytic Combinatorics