THE BASIS for course content is our textbook, which defines the field. Analytic Combinatorics aims to enable precise quantitative predictions of the properties of large combinatorial structures. The theory has emerged over recent decades as essential both for the analysis of algorithms and for the study of scientific models in many disciplines, including probability theory, statistical physics, computational biology, and information theory. With a careful combination of symbolic enumeration methods and complex analysis, drawing heavily on generating functions, results of sweeping generality emerge that can be applied in particular to fundamental structures such as permutations, sequences, strings, walks, paths, trees, graphs and maps. This account is the definitive treatment of the topic. It gives full coverage of the underlying mathematics and a thorough treatment of both classical and modern applications of the theory. The text is complemented with exercises, examples, appendices and notes to aid understanding.
Lectures in this course are based on hundreds of carefully prepared slides, which you can browse below. Clicking on a lecture title allows you to scroll through the slides for that lecture. These slides give full information about the content of the course.
All the lectures for this course are available as online videos. These are carefully prepared, integrated with course content, and produced in a studio. As with traditional in-person lectures, their purpose is to introduce topics to learners and to inspire further study.
To get an idea of what a modern online lecture video is like, try this one, the lecture on random sampling from this course. Important note: The best way to experience a lecture video is to speed it up when not interested (or bored) and slow it down when interested (or confused). You can quickly scan this video in twenty minutes or so.
All of the videos are available for viewing on the CUbits platform. This platform is recommended because it applies modern machine-learning models to build searchable transcripts, indices, and other features that enhance the experience of learning from the videos.
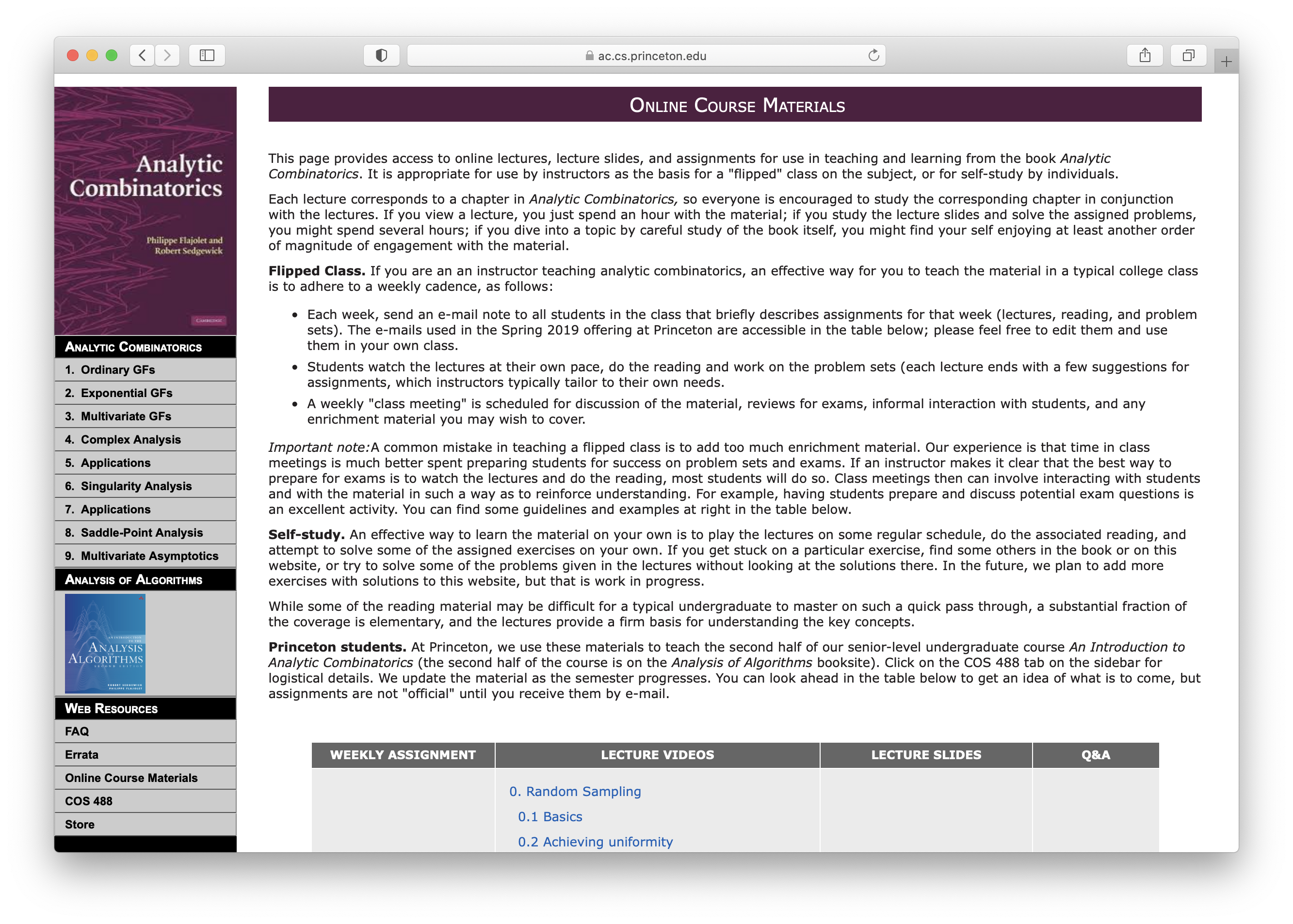
Our Analytic Combinatorics booksite is freely available on the web. It contains tens of thousands of files, is fully coordinated with our lectures and textbook and also is useful as a standalone resource. It consists of the following elements:
Excerpts. A condensed version of the text narrative.
Exercises. Selected exercises from the book and “web exercises” developed since its publication, along with some solutions.
Online course. A schedule for learning the material in the book over a seven-week period, for use either by individuals or by instructors leading a class. For example, suggested weekly e-mails to the class are included and the lecture videos and slides are integrated into the site.
This is a living resource that is constantly being improved and updated.
You can find details on how we conduct our course at Princeton on our Princeton COS 488 course website. This course is the first half of COS 488. The course website is a detailed “contract” between faculty and students, including the schedule and a full description of course components. This course has been fully online even before the pandemic. Students watch online lectures each week whenever and wherever they want and then complete and submit problem sets that challenge their understanding of the course material. Synchronization is established via weekly e-mails from the instructor delineating the assignments for the week, timely individualized feedback on assignments, and an exam on course content.